
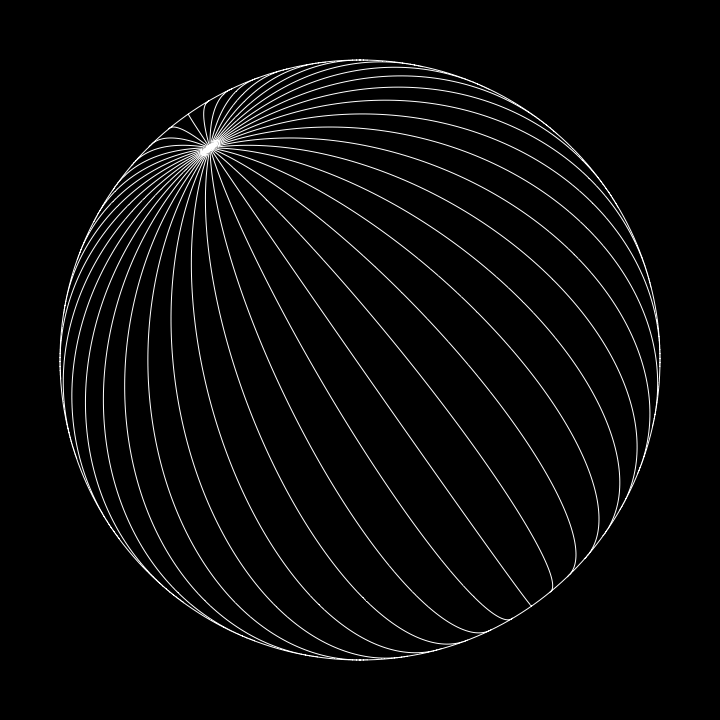
【円弧-20】では緯線を使って球を表現しましたが、今回は経線を使います。
緯線とは球の方程式が違います。(一般的な式表現とは異なり、PostScriptに変換するため乗算記号も入れています。)
[su_note note_color=”#fcfbfb” text_color=”#797979″]緯線の場合の方程式
x=r*sin(th)*sin(th2)
y=r*cos(th2)
z=r*cos(th)*sin(th2)
経線の場合の方程式
x=r*sin(th)*cos(th2)
y=r*cos(th)
z=r*sin(th)*sin(th2)[/su_note]
また緯線と違いオブジェクトが交差しているため、陰線処理が必要となります。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
%%BoundingBox: 0 0 720 720
%%HiResBoundingBox: 0 0 720 720
%%CropBox: 0 0 720 720
%%Title:緯度による球の表現
%%Creator:Studio Fruit Jam / Toyokazu Nishi
%%Copyright:Studio Fruit Jam / Toyokazu Nishi
%%CreationDate:2014年11月30日日曜日11:14:08
%%ModificationDate:2018年10月4日 木曜日21:24:04
% 数式によるパソコン・グラッフィクスのテクニック
% 著者:依田 谹(ヨダ コダマ)
% 昭和61年8月1日初版発行
% 発行所:一橋出版株式会社
% 球の方程式
% x=r*sin(th)*cos(th2)
% y=r*cos(th)
% z=r*sin(th)*sin(th2)
% ================ 座標変換 ================
360 360 translate
1 dup scale
% ================ 背景 =================
0 0 0 setrgbcolor
-360 360 720 -720 rectfill
% ================ 定義 ================
1 1 1 setrgbcolor
1 setlinewidth
/p 180 def % 円の角度
/n 20 def % 経度(縦) の数
/k p n div def % th2の角度
/xa -45 def % 球のX軸角度 a:angle
/ya -45 def % 球のY軸角度
/za 0 def % 球のZ軸角度
/r 300 def % 球のサイズ
% ================================================
% プロシージャ
% ================================================
% 図形の回転
/rotation {
% x軸角度
/x1 x def
/y1 y xa cos mul z xa sin mul sub def
/z1 y xa sin mul z xa cos mul add def
% y軸角度
/x2 x1 ya cos mul z1 ya sin mul add def
/y2 y1 def
/z2 x1 neg ya sin mul z1 ya cos mul add def
% Z軸角度
/x3 x2 za cos mul y2 za sin mul sub def
/y3 x2 za sin mul y2 za cos mul add def
/z3 z2 def
} def
% 描画
/line {
/px x3 def
/py y3 neg def
sw 1 eq { px py lineto }{ px py moveto } ifelse
/sw 1 def
} def
% ================ メイン================
newpath % パスの初期化
0 0 r 0 360 arc % 輪郭線
% ================ 球の関数 経線(縦)
0 k p { % 経線の角度
/th2 exch def
/sw 0 def % 余計な線を出さない
0 1 2 p mul { % 経線の円
/th exch def
/x r th sin mul th2 cos mul def
/y r th cos mul def
/z r th sin mul th2 sin mul def
rotation % 図形の回転
% 陰線処理 z3の負の値は回転角度によって変える
z3 -10 lt { /sw 0 def } { line } ifelse
} for
} for
stroke

陰線処理のため線のみになり、塗りつぶしができません。そこであらかじめ塗りつぶしの円を描画して、その上から経線を描画することにします。 メイン部分のみ掲載します。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
% メイン
% ================================================
newpath % パスの初期化
0.36078 0.82745 0.74901 setrgbcolor
0 0 r 0 360 arc
gsave fill % 輪郭線
grestore
0.62745 0.52941 1 setrgbcolor stroke
% ================ 球の関数 % % 緯度(横)
0 1 p 1 sub { % 緯線の角度
/th2 exch def
/sw 0 def % 余計な線を出さない
0 1 2 p mul { % 緯線の円
/th exch def
/x r th sin mul th2 cos mul def
/y r th cos mul def
/z r th sin mul th2 sin mul def
rotation % 図形の回転
% 陰線処理 z3の負の値は回転角度によって変える
z3 -10 lt { /sw 0 def } { line } ifelse
} for
} for
0.62745 0.52941 1 setrgbcolor
stroke

コメント