【曲線-11】ピーナッツカーブを描いてみよう

具象的な曲線の第三回はピーナッツカーブです。
Ceva’s trisectrixのバリエーションの一つで、b=1の時、double egg、b=2の時、bow tieと呼ばれる図形ができます。
r=1+b*sin(2*th)

(extended) Ceva’s trisectrix sextic

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%!PS-Adobe-3.0 EPSF-3.0

%%BoundingBox: 0 0 240 240

%%Title:peanut curve（ピーナッツカーブ）を描く

0 0 240 240 rectfill % 黒背景

120 120 translate % 図形を中央に移動

/b .5 def % パラメータ

/a 80 def % 大きさ



newpath % パスの初期化

0 1 360 { % 0から始めて360まで1づつ増分し{ }内を繰り返す

    /th exch def % 制御変数をth(角度)に入れる

    % ピーナッツカーブの数式

    /r 1 b 2 th mul sin mul add a mul def

    /x r th cos mul def

    /y r th sin mul def

    % thが0なら始点を置き、さもなくば線を引く

    th 0 eq { x y moveto } { x y lineto } ifelse

} for

closepath % 線を繋ぐ

1 1 1 setrgbcolor % 白色

2 setlinewidth % 線幅2ポイント

stroke % 線を描画

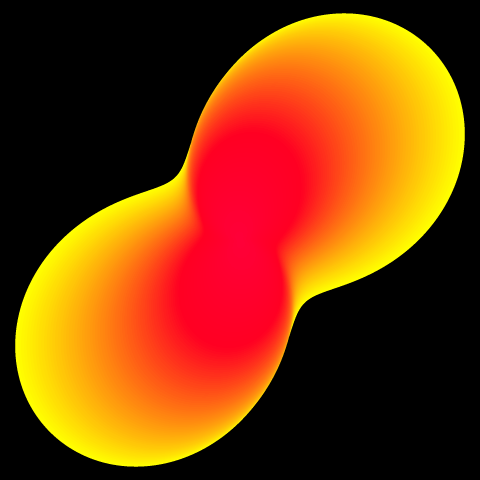
for文を追加し、aの値を変化させ、色と角度を変えてみます。
増分値（減分値）を細かくしてグラデーションにしています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
%!PS-Adobe-3.0 EPSF-3.0

%%BoundingBox: 0 0 240 240

%%Title:peanut curve（ピーナッツカーブ）を描く

0 0 240 240 rectfill % 黒背景

120 120 translate % 図形を中央に移動

/b .5 def % パラメータ

/rc 1 def % R色

/gc 1 def % G色

/bc 0 def % B色



newpath % パスの初期化

90 -.8 0 { % 90から初めて0まで-0.8減分し{ }内を繰り返す

    /a exch def % 制御変数をa(大きさ)に入れる

    .5 rotate % 0.5度回転

    0 1 360 { % 0から始めて360まで1づつ増分し{ }内を繰り返す

        /th exch def % 制御変数をth(角度)に入れる

        % ピーナッツカーブの数式

        /r 1 b 2 th mul sin mul add a mul def

        /x r th cos mul def

        /y r th sin mul def

        % thが0なら始点を置き、さもなくば線を引く

        th 0 eq { x y moveto } { x y lineto } ifelse

    } for

    closepath % 線を繋ぐ

    rc gc bc setrgbcolor % カラー設定

    fill % 塗りつぶす

    /gc gc .015 sub def % G色から0.015を引く

    /bc bc .002 add def % B色から0.002を足す

} for